Dalam kehidupan sehari-hari, kata
statistik dapat diartikan sebagai kumpulan angka-angka yang
menggambarkan suatu masalah. Statistik korban gempa kabupaten Bantul
misalnya, berisi angka-angka mengenai banyaknya korban misalnya yang
mengalami luka ringan, luka berat, dan meninggal. Contoh lain misalnya
data korban kecelakaan lalu lintas dari kantor polisi lalu lintas.
Misal:
2. Data kuantitatif, yaitu data yang berupa bilangan.
Misal:
a. Banyaknya siswa pada kelas II adalah 240.
b Tinggi pohon itu adalah 10 meter.
Menyajikan data dalam bentuk diagram
Diagram Garis
 Diagram Lingkaran
Diagram Lingkaran
Ranah privat (pengaduan) dari koran Solo Pos pada tanggal 22 Februari 2008 ditunjukkan
seperti tabel berikut.
 Nyatakan data di atas dalam bentuk diagram lingkaran.
Nyatakan data di atas dalam bentuk diagram lingkaran.
Penyelesaian
Sebelum data pada tabel di atas disajikan dengan diagram lingkaran, terlebih dahulu ditentukan besarnya sudut dalam lingkaran dari data tersebut.
1. CPNS/Honda/GTT = 5/100 x 360° = 18°
2. Perbaikan/pembangunan/gangguan jalan = 9/100 x 360° = 32,4°
3. Masalah lingkungan/kebersihan = 6/100 x 360° = 21,6°
4. Kesehatan/PKMS/Askeskin = 3/100 x 360° = 10,8°
5. Lalu lintas/penertiban jalan = 6/100 x 360° = 21,6°
6. Revitalisasi/budaya Jawa = 20/100 x 360° = 72°
7. Parkir = 3/100 x 360° = 10,8°
8. Pekat/penipuan/preman = 7/100 x 360° = 25,2°
9. Persis/olahraga = 10/100 x 360° = 36°
10. PKL/Bangunan liar = 2/100 x 360° = 7,2°
11. PLN dan PDAM = 2/100 x 360° = 7,2°
12. Provider HP = 7/100 x 360° = 25,2°
13. Tayangan TV/radio/koran = 3/100 x 360° = 10,8°
14. Lain-lain = 17/100 x 360° = 61,2°
Diagram lingkarannya adalah sebagai berikut.
 Diagram Batang
Diagram Batang
Diagram batang umumnya digunakan untuk menggambarkan perkembangan nilai suatu objek penelitian dalam kurun waktu tertentu. Diagram batang menunjukkan keterangan-keterangan dengan batang-batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah. Perhatikan contoh berikut ini.
Contoh soal
Jumlah lulusan SMA X di suatu daerah dari tahun 2001 sampai tahun 2004 adalah
sebagai berikut.
 Nyatakan data di atas dalam bentuk diagram batang.
Nyatakan data di atas dalam bentuk diagram batang.
Penyelesaian
Data tersebut dapat disajikan dengan diagram batang sebagai berikut.
 Penyajian Data dalam Bentuk Tabel Distribusi Frekuensi
Penyajian Data dalam Bentuk Tabel Distribusi Frekuensi
Perhatikan contoh data hasil nilai pengerjaan tugas Matematika
dari 40 siswa kelas XI berikut ini.
66 75 74 72 79 78 75 75 79 71
75 76 74 73 71 72 74 74 71 70
74 77 73 73 70 74 72 72 80 70
73 67 72 72 75 74 74 68 69 80
dari data diatas, dapat dibuat tabel distribusi frekuensi sbb:
 Istilah-istilah yang banyak digunakan dalam pembahasan distribusi frekuensi
Istilah-istilah yang banyak digunakan dalam pembahasan distribusi frekuensi
bergolong atau distribusi frekuensi berkelompok antara lain sebagai berikut.
a. Interval Kelas
Tiap-tiap kelompok disebut interval kelas atau sering disebut interval atau kelas
saja. Dalam contoh sebelumnya memuat enam interval ini.
65 – 67 → Interval kelas pertama
68 – 70 → Interval kelas kedua
71 – 73 → Interval kelas ketiga
74 – 76 → Interval kelas keempat
77 – 79 → Interval kelas kelima
80 – 82 → Interval kelas keenam
b. Batas Kelas
Berdasarkan tabel distribusi frekuensi di atas, angka 65, 68, 71, 74, 77, dan 80
merupakan batas bawah dari tiap-tiap kelas, sedangkan angka 67, 70, 73, 76, 79,
dan 82 merupakan batas atas dari tiap-tiap kelas.
c. Tepi Kelas (Batas Nyata Kelas)
Untuk mencari tepi kelas dapat dipakai rumus berikut ini.
Tepi bawah = batas bawah – 0,5
Tepi atas = batas atas + 0,5
Dari tabel di atas maka tepi bawah kelas pertama 64,5 dan tepi atasnya 67,5, tepi
bawah kelas kedua 67,5 dan tepi atasnya 70,5 dan seterusnya.
d. Lebar kelas
Untuk mencari lebar kelas dapat dipakai rumus:
Lebar kelas = tepi atas – tepi bawah
Jadi, lebar kelas dari tabel diatas adalah 67,5 – 64,5 = 3.
e. Titik Tengah
Untuk mencari titik tengah dapat dipakai rumus:
Titik tengah = 1/2 (batas atas + batas bawah)
Dari tabel di atas: titik tengah kelas pertama = 1/2(67 + 65) = 66
titik tengah kedua = 1/2(70 + 68) = 69
dan seterusnya.
Distribusi Frekuensi Kumulatif
Daftar distribusi kumulatif ada dua macam, yaitu sebagai berikut.
a. Daftar distribusi kumulatif kurang dari (menggunakan tepi atas).
b. Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah).
Untuk lebih jelasnya, perhatikan contoh data berikut ini.
 Dari tabel di atas dapat dibuat daftar frekuensi kumulatif kurang dari dan lebih dari seperti berikut.
Dari tabel di atas dapat dibuat daftar frekuensi kumulatif kurang dari dan lebih dari seperti berikut.
 Histogram
Histogram
sebagai berikut.
 Poligon Frekuensi
Poligon Frekuensi
Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batangbatangnya
dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas
dapat dibuat poligon frekuensinya seperti gambar berikut ini.
 contoh soal:
contoh soal:
Hasil pengukuran berat badan terhadap 100 siswa SMP X digambarkan dalam distribusi
bergolong seperti di bawah ini. Sajikan data tersebut dalam histogram dan poligon frekuensi.
 Penyelesaian
Penyelesaian
Histogram dan poligon frekuensi dari tabel di atas dapat ditunjukkan sebagai berikut.
 Poligon Frekuensi Kumulatif
Poligon Frekuensi Kumulatif
Dari distribusi frekuensi kumulatif dapat dibuat grafik garis yang disebut poligon frekuensi kumulatif. Jika poligon frekuensi kumulatif dihaluskan, diperoleh kurva yang disebut kurva ogive. Untuk lebih jelasnya, perhatikan contoh soal berikut ini.
Hasil tes ulangan Matematika terhadap 40 siswa kelas XI IPA digambarkan dalam tabel di samping.
a. Buatlah daftar frekuensi kumulatif kurang dari dan lebih dari.
b. Gambarlah ogive naik dan ogive turun.

 b. Ogive naik dan ogive turun
b. Ogive naik dan ogive turun
Daftar frekuensi kumulatif kurang dari dan lebih dari dapat disajikan dalam bidang
Cartesius. Tepi atas (67,5; 70,5; …; 82,5) atau tepi bawah (64,5; 67,5; …; 79,5)
diletakkan pada sumbu X sedangkan frekuensi kumulatif kurang dari atau frekuensi
kumulatif lebih dari diletakkan pada sumbu Y. Apabila titik-titik yang diperlukan
dihubungkan, maka terbentuk kurva yang disebut ogive. Ada dua macam ogive,
yaitu ogive naik dan ogive turun. Ogive naik apabila grafik disusun berdasarkan
distribusi frekuensi kumulatif kurang dari. Sedangkan ogive turun apabila berdasarkan
distribusi frekuensi kumulatif lebih dari.
Ogive naik dan ogive turun data di atas adalah sebagai berikut.

Statistik juga diartikan sebagai suatu
ukuran yang dihitung dari sekumpulan data dan merupakan wakil dari data
itu. Misalnya rata-rata skor tes matematika kelas XI adalah 78 atau
benda lebih dari 90% penduduk Indonesia berada di pedesaan. Sedangkan
pengertian statistika sesungguhnya adalah pengetahuan yang berhubungan
dengan cara penyusunan data, penyajian data, dan penarikan kesimpulan
mengenai suatu keseluruhan berdasarkan data yang ada pada bagian dari
keseluruhan tadi. Keseluruhan objek yang diteleti disebut populasi
sedangkan bagian dari populasi disebut sampel.
Menurut fungsinya, statistika
dibedakan menjadi dua jenis, yaitu statistika deskriptif dan statistika
induktif (inferensial). Statistika deskriptif adalah bagian statistika
yang mempelajari cara penyusunan dan penyajian data yang dikumpulkan.
Penyusunan data dimaksudkan untuk memberikan gambaran mengenai urutan
data atau kelompok data, sehingga pengguna data dapat mengenalinya
dengan mudah. Penyajian data dimaksudkan untuk memberikan gambaran
mengenai data atau kelompok data dalam bentuk tabel, diagram, atau
gambar.
Statistika induktif atau inferensial adalah bagian statistika yang mempelajari tata cara penarikan kesimpulan yang valid mengenai populasi berdasarkan data pada sampel. Dalam menarik kesimpulan pada statistika inferensial biasanya digunakan unsur peluang.
Statistika induktif atau inferensial adalah bagian statistika yang mempelajari tata cara penarikan kesimpulan yang valid mengenai populasi berdasarkan data pada sampel. Dalam menarik kesimpulan pada statistika inferensial biasanya digunakan unsur peluang.
Bila membicarakan statistika, maka
tidak lepas dengan apa yang disebut data. Data dapat diartikan sebagai
keterangan yang diperlukan untuk memecahkan suatu masalah. Berikut
ini diberikan macam-macam data ditinjau menurut sifatnya, yaitu:
1. Data kualitatif, yaitu data yang berbentuk kategori atau atribut.Misal:
a. Harga mobil semakin terjangkau
b. Murid-murid di SD Negeri 3 rajin-rajin.2. Data kuantitatif, yaitu data yang berupa bilangan.
Misal:
a. Banyaknya siswa pada kelas II adalah 240.
b Tinggi pohon itu adalah 10 meter.
Menyajikan data dalam bentuk diagram
Diagram Garis
Penyajian data statistik dengan
menggunakan diagram berbentuk garis lurus disebut diagram garis lurus
atau diagram garis. Diagram garis biasanya digunakan untuk menyajikan
data statistik yang diperoleh berdasarkan pengamatan dari waktu ke waktu
secara berurutan.
Sumbu X menunjukkan waktu-waktu
pengamatan, sedangkan sumbu Y menunjukkan nilai data pengamatan untuk
suatu waktu tertentu. Kumpulan waktu dan pengamatan membentuk
titik-titik pada bidang XY, selanjutnya kolom dari tiap dua titik yang
berdekatan tadi dihubungkan dengan garis lurus sehingga akan diperoleh
diagram garis atau grafik garis. Untuk lebih jelasnya, perhatikan contoh
soal berikut.

Diagram lingkaran adalah penyajian
data statistik dengan menggunakan gambar yang berbentuk lingkaran.
Bagian-bagian dari daerah lingkaran menunjukkan bagian bagian atau
persen dari keseluruhan. Untuk membuat diagram lingkaran, terlebih
dahulu ditentukan besarnya persentase tiap objek terhadap keseluruhan
data dan besarnya sudut pusat sektor lingkaran.
Contoh soalRanah privat (pengaduan) dari koran Solo Pos pada tanggal 22 Februari 2008 ditunjukkan
seperti tabel berikut.

Penyelesaian
Sebelum data pada tabel di atas disajikan dengan diagram lingkaran, terlebih dahulu ditentukan besarnya sudut dalam lingkaran dari data tersebut.
1. CPNS/Honda/GTT = 5/100 x 360° = 18°
2. Perbaikan/pembangunan/gangguan jalan = 9/100 x 360° = 32,4°
3. Masalah lingkungan/kebersihan = 6/100 x 360° = 21,6°
4. Kesehatan/PKMS/Askeskin = 3/100 x 360° = 10,8°
5. Lalu lintas/penertiban jalan = 6/100 x 360° = 21,6°
6. Revitalisasi/budaya Jawa = 20/100 x 360° = 72°
7. Parkir = 3/100 x 360° = 10,8°
8. Pekat/penipuan/preman = 7/100 x 360° = 25,2°
9. Persis/olahraga = 10/100 x 360° = 36°
10. PKL/Bangunan liar = 2/100 x 360° = 7,2°
11. PLN dan PDAM = 2/100 x 360° = 7,2°
12. Provider HP = 7/100 x 360° = 25,2°
13. Tayangan TV/radio/koran = 3/100 x 360° = 10,8°
14. Lain-lain = 17/100 x 360° = 61,2°
Diagram lingkarannya adalah sebagai berikut.

Diagram batang umumnya digunakan untuk menggambarkan perkembangan nilai suatu objek penelitian dalam kurun waktu tertentu. Diagram batang menunjukkan keterangan-keterangan dengan batang-batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah. Perhatikan contoh berikut ini.
Contoh soal
Jumlah lulusan SMA X di suatu daerah dari tahun 2001 sampai tahun 2004 adalah
sebagai berikut.

Penyelesaian
Data tersebut dapat disajikan dengan diagram batang sebagai berikut.

Perhatikan contoh data hasil nilai pengerjaan tugas Matematika
dari 40 siswa kelas XI berikut ini.
66 75 74 72 79 78 75 75 79 71
75 76 74 73 71 72 74 74 71 70
74 77 73 73 70 74 72 72 80 70
73 67 72 72 75 74 74 68 69 80
dari data diatas, dapat dibuat tabel distribusi frekuensi sbb:

bergolong atau distribusi frekuensi berkelompok antara lain sebagai berikut.
a. Interval Kelas
Tiap-tiap kelompok disebut interval kelas atau sering disebut interval atau kelas
saja. Dalam contoh sebelumnya memuat enam interval ini.
65 – 67 → Interval kelas pertama
68 – 70 → Interval kelas kedua
71 – 73 → Interval kelas ketiga
74 – 76 → Interval kelas keempat
77 – 79 → Interval kelas kelima
80 – 82 → Interval kelas keenam
b. Batas Kelas
Berdasarkan tabel distribusi frekuensi di atas, angka 65, 68, 71, 74, 77, dan 80
merupakan batas bawah dari tiap-tiap kelas, sedangkan angka 67, 70, 73, 76, 79,
dan 82 merupakan batas atas dari tiap-tiap kelas.
c. Tepi Kelas (Batas Nyata Kelas)
Untuk mencari tepi kelas dapat dipakai rumus berikut ini.
Tepi bawah = batas bawah – 0,5
Tepi atas = batas atas + 0,5
Dari tabel di atas maka tepi bawah kelas pertama 64,5 dan tepi atasnya 67,5, tepi
bawah kelas kedua 67,5 dan tepi atasnya 70,5 dan seterusnya.
d. Lebar kelas
Untuk mencari lebar kelas dapat dipakai rumus:
Lebar kelas = tepi atas – tepi bawah
Jadi, lebar kelas dari tabel diatas adalah 67,5 – 64,5 = 3.
e. Titik Tengah
Untuk mencari titik tengah dapat dipakai rumus:
Titik tengah = 1/2 (batas atas + batas bawah)
Dari tabel di atas: titik tengah kelas pertama = 1/2(67 + 65) = 66
titik tengah kedua = 1/2(70 + 68) = 69
dan seterusnya.
Distribusi Frekuensi Kumulatif
Daftar distribusi kumulatif ada dua macam, yaitu sebagai berikut.
a. Daftar distribusi kumulatif kurang dari (menggunakan tepi atas).
b. Daftar distribusi kumulatif lebih dari (menggunakan tepi bawah).
Untuk lebih jelasnya, perhatikan contoh data berikut ini.


Dari suatu data yang diperoleh dapat
disusun dalam tabel distribusi frekuensi dan disajikan dalam bentuk
diagram yang disebut histogram. Jika pada diagram batang, gambar
batang-batangnya terpisah maka pada histogram gambar batang-batangnya
berimpit. Histogram dapat disajikan dari distribusi frekuensi tunggal
maupun distribusi frekuensi bergolong. Untuk lebih jelasnya, perhatikan
contoh berikut ini.
Data banyaknya siswa kelas XI IPA yang tidak masuk sekolah dalam 8 hari berurutansebagai berikut.

Apabila pada titik-titik tengah dari histogram dihubungkan dengan garis dan batangbatangnya
dihapus, maka akan diperoleh poligon frekuensi. Berdasarkan contoh di atas
dapat dibuat poligon frekuensinya seperti gambar berikut ini.

Hasil pengukuran berat badan terhadap 100 siswa SMP X digambarkan dalam distribusi
bergolong seperti di bawah ini. Sajikan data tersebut dalam histogram dan poligon frekuensi.

Histogram dan poligon frekuensi dari tabel di atas dapat ditunjukkan sebagai berikut.

Dari distribusi frekuensi kumulatif dapat dibuat grafik garis yang disebut poligon frekuensi kumulatif. Jika poligon frekuensi kumulatif dihaluskan, diperoleh kurva yang disebut kurva ogive. Untuk lebih jelasnya, perhatikan contoh soal berikut ini.
Hasil tes ulangan Matematika terhadap 40 siswa kelas XI IPA digambarkan dalam tabel di samping.
a. Buatlah daftar frekuensi kumulatif kurang dari dan lebih dari.
b. Gambarlah ogive naik dan ogive turun.


Daftar frekuensi kumulatif kurang dari dan lebih dari dapat disajikan dalam bidang
Cartesius. Tepi atas (67,5; 70,5; …; 82,5) atau tepi bawah (64,5; 67,5; …; 79,5)
diletakkan pada sumbu X sedangkan frekuensi kumulatif kurang dari atau frekuensi
kumulatif lebih dari diletakkan pada sumbu Y. Apabila titik-titik yang diperlukan
dihubungkan, maka terbentuk kurva yang disebut ogive. Ada dua macam ogive,
yaitu ogive naik dan ogive turun. Ogive naik apabila grafik disusun berdasarkan
distribusi frekuensi kumulatif kurang dari. Sedangkan ogive turun apabila berdasarkan
distribusi frekuensi kumulatif lebih dari.
Ogive naik dan ogive turun data di atas adalah sebagai berikut.

Semoga Bermanfaat :-)
 19.53
19.53
 Unknown
Unknown




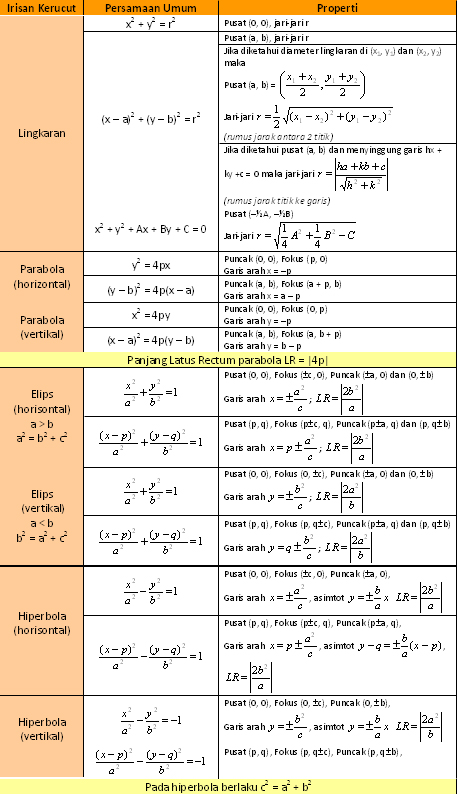



 atau Pn,r
atau Pn,r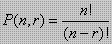
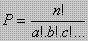
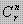 atau Cn,r
atau Cn,r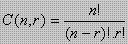
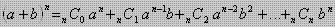
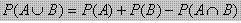
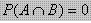 maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
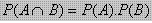
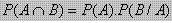

![clip_image013[9] clip_image013[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi5vyUX_bN-v-YDFyCYaWoYwlYzo1-QKk_7ZUHkkyc2-fYnyp2K9V-wJWk4OKfzieCWQyxi8Mm-P-IzdWyqD3kfgkDvccyS9f4L3SXKXe93ad-G68P_eUgwgoEfskHbgPuASxnKG0AnApcm/?imgmax=800)
![clip_image035[9] clip_image035[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEil63SP15QNB5y0N_P_jKEOoTmMnbiuTwjrVZ1rru0iP9IXCOjRIFY6Va9rVfnQurXaQaX433GwUU0f0yp4-zJoDj3d265jJZVjOEguWCal_W-aSvLUCZrf82cajUcpvR8aCpsopglOMMf7/?imgmax=800)


